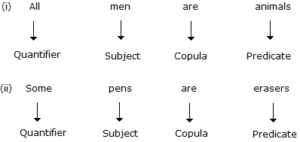
In Logic, any categorical statement is termed as the Proposition. A Proposition (or a categorical statement) is a statement that asserts that either a part of, or the whole of, one set of objects – the set identified by the subject term in the sentence expressing that statement – either is included in, or is excluded from, another set – the set identified by the predicate term in that sentence. The standard form of a proposition is : Quantifier + Subject + Copula + Predicate Thus, the proposition consists of four parts : 1. Quantifier: The words ‘all’, ‘no’ and ‘some’ are called quantifiers because they specify a quantity ‘All’ and ‘no’ are universal quantifiers because they refer to every object in a certain set, while the quantifier ‘some’ is a particular quantifier because it refers to at least one existing object in a certain set. 2. Subject (denoted by ‘S’): The subject is that about which something is said. 3. Predicate (denoted by ‘P’): The predicate is the part of the proposition denoting that which is affirmed or denied about the subject. 4. Copula : The copula is that part of the proposition which denotes the relation between the subject and the predicate. Examples:
Four-Fold Classification of Propositions : A proposition is said to have a universal quantity if it begins with a universal quantifier, and a particular quantity if it begins with a particular quantifier. Besides, propositions which assert something about the inclusion of the whole or a part of one set in the other are said to have affirmative quality, while those which deny the inclusion of the whole or a part of one set in the other are said to have a negative quality. Also, a term is distributed in a proposition if it refers to all members of the set of objects denoted by that term. Otherwise, it is said to be undistributed. Based on the above facts, propositions can be classified into four types : 1. Universal Affirmative Proposition (denoted by A): It distributes only the subject i.e. the predicate is not interchangeable with the subject while maintaining the validity of the proposition. e.g., All snakes are reptiles. This is proposition A since we cannot say ‘All reptiles are snakes’. 2. Universal Negative Proposition (denoted by E): It distributes both the subject and the predicate i.e. an entire class of predicate term is denied to the entire class of the subject term, as in the proposition. e.g., No boy is intelligent. 3.Particular Affirmative Proposition (denoted by I): It distributes neither the subject nor the predicate. e.g.,Some men are foolish. Here, the subject term ‘men’ is used not for all but only for some men and similarly the predicate term ‘foolish’ is affirmed for a part of subject class. So, both are undistributed. 4. Particular Negative Proposition (denoted by O): It distributes only the predicate. e.g., Some animals are not wild. Here, the subject term ‘animals’ is used only for a part of its class and hence is undistributed while the predicate term ‘wild’ is denied in entirety to the subject term and hence is distributed. These facts can be summarized as follows :
Statement Form Quantity Quality Distributed
(A): All S is P. Universal Affirmative S only
(E): No S is P. Universal Negative Both S and P
(I): Some S is P. Particular Affirmative Neither S nor P
(O): Some S is not P Particular Negative P only Logical Deduction: The phenomenon of deriving a conclusion from a single proposition or a set of given propositions, is known as logical deduction. The given propositions are also referred to as the premises. Two Inferential Processes of Deduction : I. Immediate Deductive Inference : Here, conclusion is deduced from one of the given propositions, by any of the three ways -conversion, obversion and contraposition. 1. Conversion: The Conversion proceeds with interchanging the subject term and the predicate term i.e. the subject term of the premise becomes the predicate term of the conclusion and the predicate term of the premise becomes the subject of the conclusion. The given proposition is called convertend, whereas the conclusion drawn from it is called its converse. Table of Valid Conversions
Convertend Converse
A: All S is P Ex. All pins are tops. I: Some P is S Some tops are pins.
E: No S is P. Ex. No fish is whale. E: No P is S. No whale is fish.
I: Some S is P. Ex. Some boys are poets. I: Some P is S. Some poets are boys.
O: Some S is not P. No valid conversionNote that in a conversion, the quality remains the same and the quantity may change. 2. Obversion: In obversion, we change the quality of the proposition and replace the predicate term by its complement. Table of Valid Obversions
Obvertend Obverse
A: All birds are mammals. E: No birds are non-mammals.
E: No poets are singers. A: All poets are non-singers.
I: Some nurses are doctors. O: Some nurses are not non-doctors.
O: some politicians are not statesmen. I: Some politicians are non-statesmen.3. Contraposition: To obtain the contrapositive of a statement, we first replace the subject and predicate terms in the proposition and then exchange both these terms with their complements. Table of Valid Contrapositions
Proposition Contrapositive
A: All birds are mammals. A: All non-mammals are non-birds.
I: Some birds are mammals. I: Some non-mammals are non-birds.
Note: The valid converse, obverse or contrapositive of a given proposition always logically follows from the proposition. II. Mediate Deductive Inference (SYLLOGISM): First introduced by Aristotle, a Syllogism is a deductive argument in which conclusion has to be drawn from two propositions referred to as the premises. Example: 1. All lotus are flowers. 2. All flowers are beautiful. 3. All lotus are beautiful. Clearly, the propositions 1 and 2 are the premises and the proposition 3, which follows from the first two propositions, is called the conclusion. Term : In Logic, a term is a word or a combination of words, which by itself can be used as a subject or predicate of a proposition. Syllogism is concerned with three terms : 1. Major Term : It is the predicate of the conclusion and is denoted by P (first letter of ‘Predicate’). 2. Minor Term: It is the subject of the conclusion and is denoted by S (first letter of ‘Subject’). 3. Middle Term: It is the term common to both the premises and is denoted by M (first letter of ‘Middle’). Example: Premises: 1. All dogs are animals. 2. All tigers are dogs. Conclusion : All tigers are animals. Here ‘animals’ is the predicate of the conclusion and so,.it is the major term. P. ‘Tigers’ is the subject of the conclusion and so, it is the minor term, S. ‘Dogs’ is the term common to both the premises and so, it is the middle term, M. Major And Minor Premises : Of the two premises, the major premise is that in which the middle term is the subject and the minor premise is that in which the middle term is the predicate. RULES FOR DERIVING CONCLUSION FROM TWO GIVEN PREMISES: 1. The conclusion does not contain the middle term. Example. Statements : 1. All men are girls. 2. Some girls are students. Conclusions : 1. All girls are men. 2. Some girls are not students. Since both the conclusions 1 and 2 contain the middle term ‘girls’, so neither of them can follow.
2. No term can be distributed in the conclusion unless it is distributed in the premises. Example. Statements : 1. Some dogs are goats. 2. All goats are cows. Conclusions : 1. All cows are goats. 2. Some dogs are cows. Statement 1 is an I-type proposition which distributes neither the subject nor the predicate. Statement 2 is an A type proposition which distributes the subject i.e. ‘goats’ only. Conclusion 1 is an A-type proposition which distributes the subject ‘cow’ only Since the term ‘cows’ is distributed in conclusion 1 without being distributed in the premises, so conclusion 1 cannot follow.
3. The middle term (M) should he distributed at least once in the premises. Otherwise, the conclusion cannot follow. For the middle term to be distributed in a premise. (i) M must be the subject if premise is an A proposition. (ii) M must be subject or predicate if premise is an E proposition. (iii) M must be predicate if premise is an O proposition. Note that in an I proposition, which distributes neither the subject nor the predicate, the middle term cannot be distributed. Example. Statements : 1. All fans are watches. 2. Some watches are black. Conclusions : 1. All watches are fans. 2. Some fans are black. In the premises, the middle term is ‘watches’. Clearly, it is not distributed in the first premise which is an A proposition as it does not form its subject. Also, it is not distributed in the second premise which is an I proposition. Since the middle term is not distributed even once in the premises, so no conclusion follows.
4. No conclusion follows (a) if both the premises are particular Example. Statements : 1. Some books are pens. 2. Some pens are erasers. Conclusions: 1. All books are erasers. 2. Some erasers are books. Since both the premises are particular, so no definite conclusion follows. (b) if both the premises are negative. Example. Statements : 1. No flower is mango. 2. No mango is cherry. Conclusions : 1. No flower is cherry. 2. Some cherries are mangoes. Since both the premises are negative, neither conclusion follows. (c) if the major premise is particular and the minor premise is negative. Example. Statements: 1. Some dogs are bulls. 2. No tigers are dogs. Conclusions: 1. No dogs are tigers. 2. Some bulls are tigers. Here, the first premise containing the middle term ‘dogs’ as the subject is the major premise and the second premise containing the middle term ‘dogs’ as the predicate is the minor premise. Since the major premise is particular and the minor premise is negative, so no conclusion follows.
5. If the middle term is distributed twice, the conclusion cannot be universal. Example. Statements : 1. All fans are chairs. 2. No tables are fans. Conclusions: 1. No tables are chairs. 2. Some tables are chairs. Here, the first premise is an A proposition and so, the middle term ‘fans’ forming the subject is distributed. The second premise is an E proposition and so, the middle term ‘fans’ forming the predicate is distributed. Since the middle term is distributed twice, so the conclusion cannot be universal.
6. If one premise is negative, the conclusion must be nega
tive. Example. Statements: 1. All grasses are trees. 2. No tree is shrub. Conclusions: 1. No grasses are shrubs. 2. Some shrubs are grasses. Since one premise is negative, the conclusion must be negative. So, conclusion 2 cannot follow.
7. If one premise is particular, the conclusion must be particular. Example. Statements: 1. Some boys are thieves. 2. All thieves are dacoits. Conclusions : 1. Some boys are dacoits. 2. All dacoits are boys. Since one premise is particular, the conclusion must be particular. So, conclusion 2 cannot follow.
8. If both the premises are affirmative, the conclusion must be affirmative. Example. Statements : 1. All women are mothers. 2. All mothers are sisters. Conclusions : 1. All women are sisters. 2. Some women are not sisters. Since both the premises are affirmative, the conclusion must be affirmative. So, conclusion 2 cannot follow.
9. If both the premises are universal, the conclusion must be universal. Complementary pair: A pair of contradictory statements i.e. a pair of statements such that if one is true, the other is false and when no definite conclusion can be drawn, either of them is bound to follow, is called a complementary pair. E and I-type propositions together form a complementary pair and usually either of them follows, in a case where we cannot arrive at a definite conclusion, using the rules of syllogism. Let us study the various possible cases and draw all possible inferences in each case, along with verification through Venn diagrams. Case 1: All men are boys. All boys are students. Immediate Deductive Inferences: The converse of first premise i.e. ‘Some boys are men’ and the converse of second premise i.e. ‘Some students are boys’ both hold. Mediate Deductive Inferences: Since both the premises are universal and affirmative, the conclusion must be universal affirmative. Also, the conclusion should not contain the middle term. So, it follows that ‘All men are students’. The converse of this conclusion i.e. ‘Some students are men’ also holds.

Case 2:
All birds are animals. All fishes are animals. Immediate Deductive Inferences: The converse of first premise i.e. ‘Some animals are birds’ and the converse of second premise i.e. ‘Some animals are fishes’ both hold. Mediate Deductive Inferences: Both, being A-type propositions, distribute subject only. Thus, the middle term ‘animals’ is not distributed even once in the premises. So, no definite conclusion follows.

Case 3:
All puppets are dolls. Some dolls are rattles. Immediate Deductive Inferences: The converse of the first premise i.e. ‘Some dolls are puppets’ and the converse of the second premise i.e. ‘Some rattles are dolls’, both hold. Mediate Deductive Inferences: First premise, being an A-type proposition, distributes the subject only while the second premise, being an I-type proposition, distributes neither subject nor predicate. Since the middle term ‘dolls’ is not distributed even once in the premises, so no definite conclusion can be drawn.
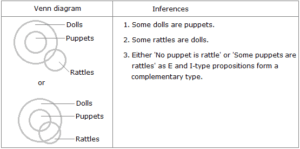
Case 4:
Some writers are players. All players are musicians. Immediate Deductive Inferences : The converse of the first premise i.e. ‘Some players are writers’ and the converse of the second premise i.e. ‘Some musicians are players’, both hold. Mediate Deductive Inferences: Since one premise is particular, the conclusion must be particular and should not contain the middle term. So, it follows that ‘Some writers are musicians’. The converse of this conclusion i.e. ‘Some musicians are writers’ also holds.

Case 5:
All boxes are toys. Some boxes are clips. Immediate Deductive Inferences : The converse of the first premise i.e. ‘Some toys are boxes’ and the converse of the second premise i.e. ‘Some clips are boxes’, both hold. Mediate Deductive Inferences: Since one premise is particular, the conclusion must be particular and should not contain the middle term. So, it follows that ‘Some toys are clips’. The converse of this conclusion i.e. ‘Some clips are toys’ also holds.
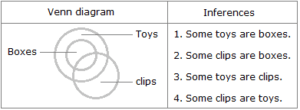
Case 6:
All buses are vans. Some cycles are vans. Immediate Deductive Inferences: The converse of the first premise i.e. ‘Some vans are buses’ and the converse of the second premise i.e. ‘Some vans are cycles’, both hold. Mediate Deductive Inferences: First premise, being an A-type proposition, distributes subject only and the second premise, being an I-type proposition, distributes neither subject nor predicate. So, the middle term ‘vans’ is not distributed even once in the premises. Hence, no definite conclusion can be drawn.
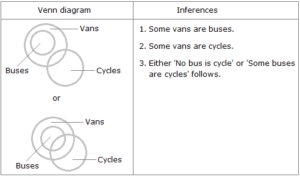
Case 7:
Some radios are cameras. Some cameras are statues. Immediate Deductive Inferences: The converse of the first premise i.e. ‘Some cameras are radios’ and the converse of the second premise i.e. ‘Some statues are cameras’, both hold. Mediate Deductive Inferences : Since both premises are particular, no definite conclusion follows.

Case 8:
All cakes are candies. No candy is pastry. Immediate Deductive Inferences: The converse of the first premise i.e. ‘Some candies are cakes’ and the converse of the second premise i.e. ‘No pastry is candy’, both hold. Mediate Deductive Inferences: Since both premises are universal, the conclusion must be universal. Since one premise is negative, the conclusion must be negative. So, it follows that ‘No cake is pastry’. The converse of this conclusion i.e. ‘No pastry is cake’ also holds.
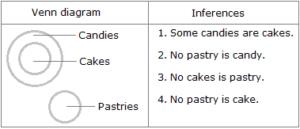
Case 9:
No coin is ring. All rings are bangles. Immediate Deductive Inferences : The converse of the first premise i.e. ‘No ring is coin’ and the converse of the second premise i.e.’Some bangles are rings’, both hold. Mediate Deductive Inferences: First premise, being an E-type proposition, distributes both the subject and the predicate. Second premise, being an A-type proposition, distributes the subject. Thus, the middle term ‘ring’ is distributed twice in the premises. So, the conclusion cannot be universal. Also, since one premise is negative, the conclusion must be negative. Thus, the conclusion must be particular negative i.e. O-type. So, it follows that ‘some bangles are not coins’.

Case 10:
Some lamps are candles. No candle is bulb. Immediate Deductive Inferences : The converse of the first premise i.e. ‘Some candles are lamps’ and the converse of the second premise i.e. ‘No bulb is candle’, both hold. Mediate Deductive Inferences: Since one premise is particular and the other negative, the conclusion must be particular negative i.e. O-type, So, it follows that ‘Some lamps are not bulbs’.

Important Points To Remember:
While deriving logical conclusions, always remember that the following conclusions hold : 1. The converse of each of the given premises; 2. The conclusion that directly follows from the given premises in accordance with the rules of syllogism; 3. The converse of the derived conclusions.

